Molecular Dynamics: Bonded interactions

 

Building a Molecular Mechanics (MM) model of a microscopic system has become a standard practice in modern computational chemistry. This process requires us to compute the potential energy of the molecule at a given configuration $R$. Overall, the energy is computed as the sum of two contributions $E_{bond}$, and $E_{non-bond}$:

 

$$E_{MM}(R) = E_{bond} + E_{non-bond}$$

 

Non-bonding terms have already been addressed in other articles. Here we focus on the different contributions constituting the so-called bonding interactions. More specifically, $E_{bond}$ is the sum of four terms (i) stretching $E_{str}$, (ii) bending $E_{bend}$, (iii) torsions $E_{tors}$, (iv) cross terms $E_{cross}$.

 

$$E_{bond} = E_{str}+E_{bend}+E_{tors}+E_{cross}$$

 

Below you can find a more detailed description of each term.

 

Stretching terms

 

Stretching terms take into account the sum of all the 1-2 interactions in a molecule, namely the bonds (Figure 1).

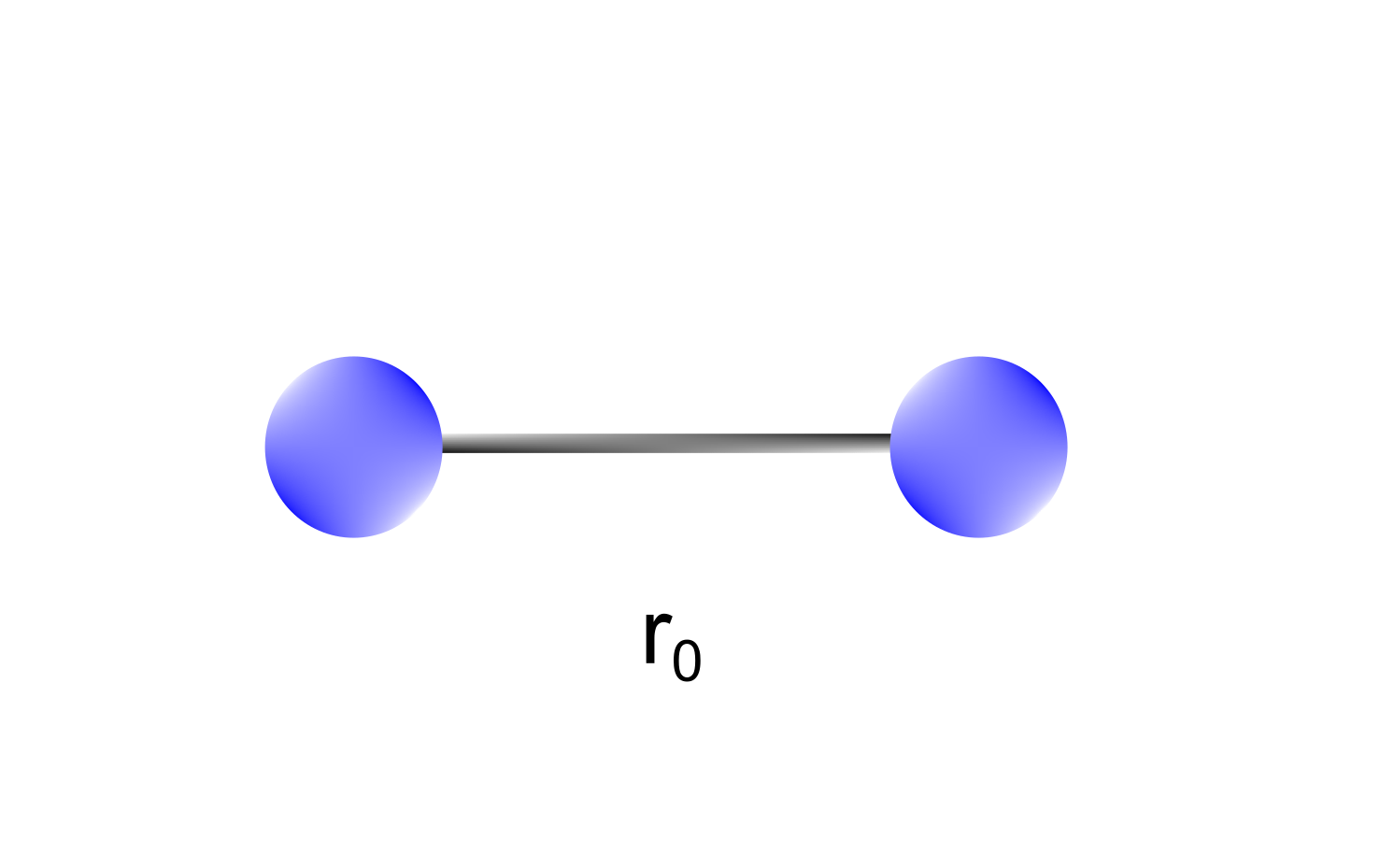
Figure 1 Stretching terms depend on 1-2 interactions between atoms (bond lengths). A bond between two atoms is characterized by an equilibrium bond length representing the most stable configuration.

In MM the bonding energy between different atom types can be expressed as a Taylor expansion around the equilibrium bond length.

 

$$E_{str} = \sum_{i}\frac{k_i}{2}(l_i - l_{i,0})^2$$

 

Where the Taylor expansion is truncated at the first term and the sum is over every bond ($i$). The equation is composed of parameters and variables.

Consequently, for the $i$-th atom type characterized by bond length $l_i$ we use the two parameters $l_{i,0}$ and $k_i$.

The result is that the potential of our model is approximated through the harmonic oscillator and it corresponds to the parabola that best fits the experimental data. The approximation is particularly valid in the region close to the minimum where the energy can be approximated as quadratic. However, it can easily break down as the bond length elongates and gets far from equilibrium. If we need a more accurate description we can add other terms to the Taylor expansion (cubic, quartic…).

 

$$E_{str} = \sum_{i}\frac{k_1}{2}(l_i - l_{i,0})^2 - \frac{k_2}{2}(l_i - l_{i,0})^3 + \frac{k_3}{2}(l_i - l_{i,0})^4$$

 

This method is not capable of describing the actual behavior of a molecule because the function does not converge to the dissociation energy value at $+\infty$.

The function that is able to correctly describe the dissociation of a diatomic molecule is the well-known Morse potential. This curve describes how the potential changes as a function of the bond length, and it is expressed as follows:

 

$$E_{morse} = D_e[1- e^{(-\alpha^(l_i-l_i^0)}]^2$$

 

Where $D_e$ is the dissociation energy and $\alpha$ is related to the force constant so that:

 

$$\alpha = \sqrt{\left(\frac{k}{2D_e}\right)}$$

 

However, the Morse potential is not used because it exhibits a larger number of parameters that negatively affect the computational cost.

However, its expression is extremely complicated to compute because it involves a larger number of parameters that negatively affect the computational cost.

 

Bending terms

 

Bending terms takes into account the sum of all the 1-3 interactions in a molecule, namely the angles formed between atoms (Figure 2). Similar to what we saw for stretching terms, in MM the energy required to bend an angle ($E_{bend}$) is expanded as a Taylor series around an equilibrium bond angle. Also in this case, the series is expressed up to the second term, and the system is modeled through the harmonic oscillator approximation.

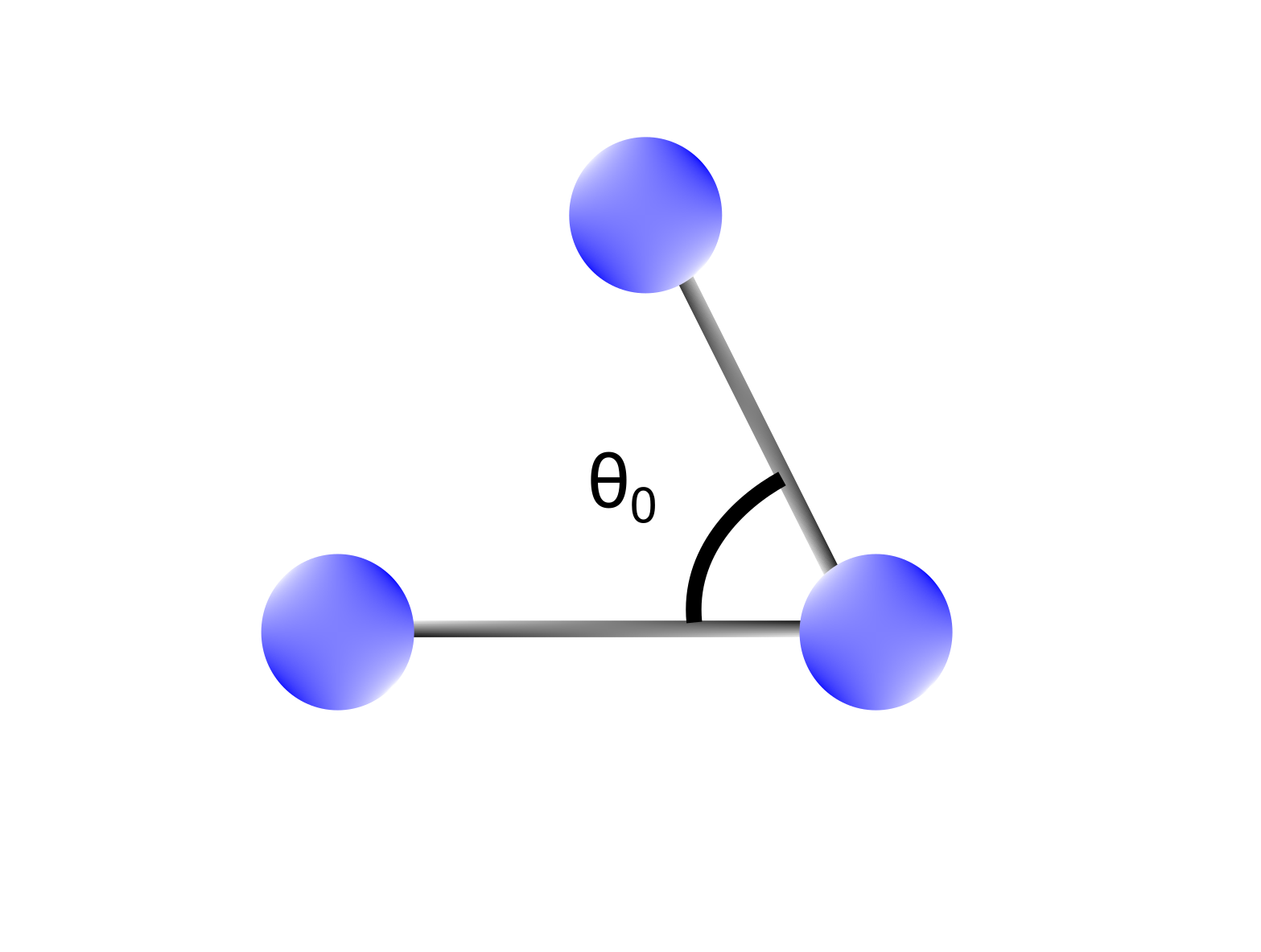
Figure 2 Bending terms depend on 1-3 interactions between atoms (bond angles). A bond between two atoms is characterized by an equilibrium bond angle ($\theta_0$) representing the most stable configuration.

 

$$E_{bend} = \sum_{angles}\frac{k_i}{2}(\theta_i - \theta_{i,0})^2$$

 

While the simple harmonic expansion is adequate for most applications, there may be cases where higher accuracy is required. The next improvement is to include a third-order term.

 

$$E_{bend} = \sum_{angles}\frac{k_1}{2}(\theta_i - \theta_{i,0})^2 + \frac{k_2}{2}(\theta_i - \theta_{i,0})^6$$

 

Torsional terms

 

The torsional terms ($E_{str}$) are needed to describe the change in potential energy as a function of the dihedral angles arising from 1-4 interactions in a molecule. In other words, considering a four atom sequence $A-B-C-D$, these contributions account for the rotations around the $B-C$ bond.

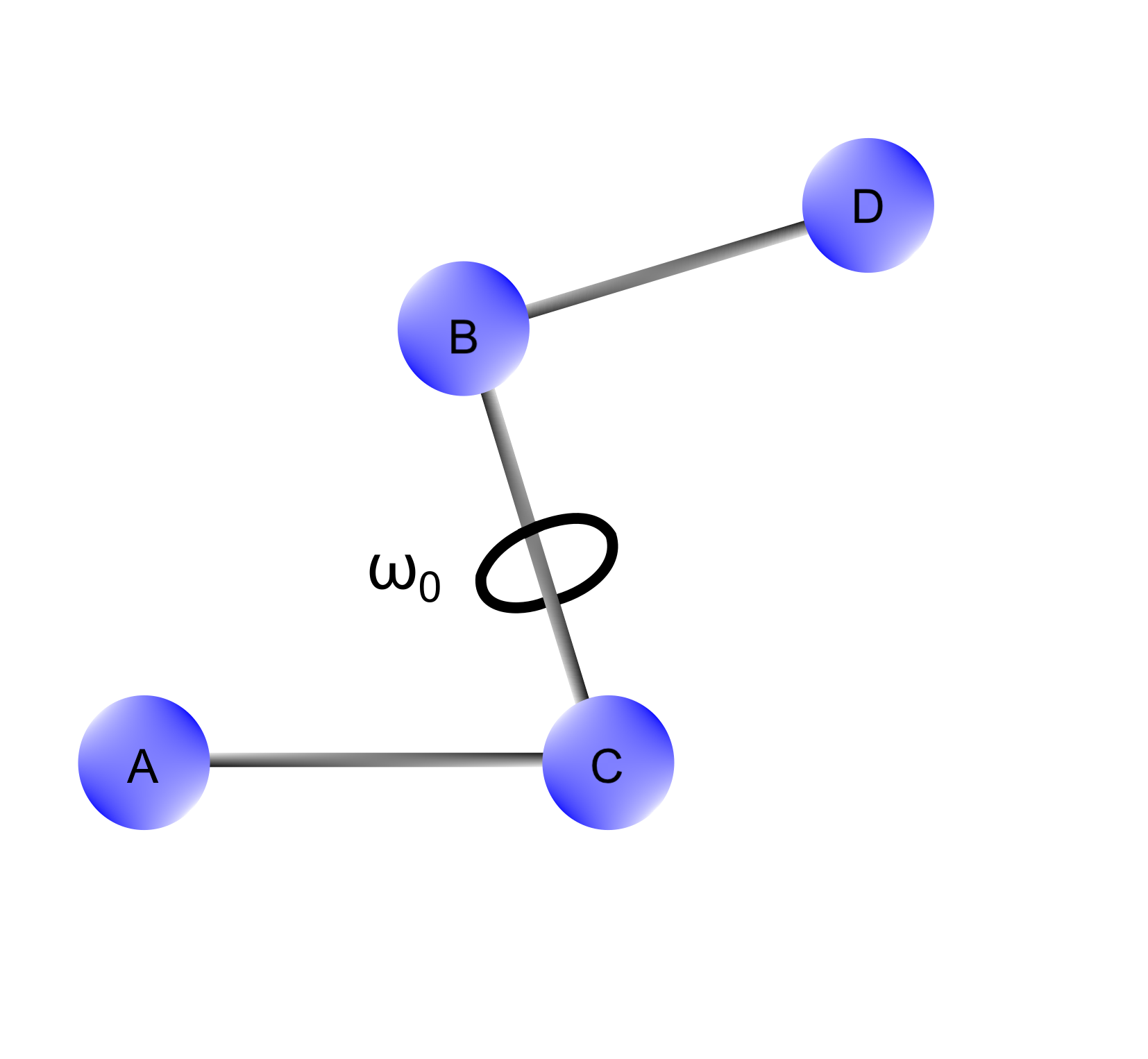
Figure 4 The dihedral angle ($\omega$) is the angle formed between $A$ and $D$

The expression for the torsional potential is the following:

 

$$E_{tors} = \sum_{tors}\sum_{n} \frac{V_n}{2}(1 + cos(n\omega - \gamma))$$

 

The torsional energy function must be periodic in the angle $\omega$. In other words, after a 360° rotation the energy is expected to return to its original value. The term $n$ describes the periodicity of the function.

• $n = 1$ The rotation is periodic by 360°

• $n = 2$ The function is composed of two repetitions and, therefore, the period is 180°

• $n = 3$ We have three barriers and the function repeats itself every 120°  

  $\vdots$

The value of $n$ depends on the structure of the molecule.

 

 

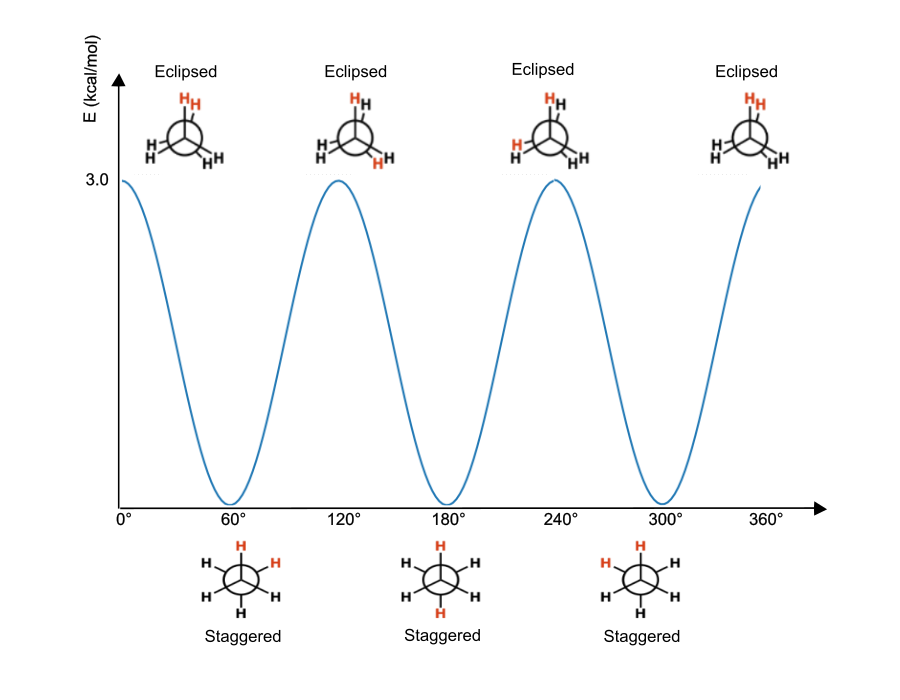
Figure 5. Torsional energy diagram for ethane which displays a three-fold repetition ($n=3$).

In the above example, we can see how the energy of an ethane molecule changes as a function of the $C-C$ dihedral angle. We can instantly notice that the barrier to rotation ($V_n$) is about 3.0 kcal/mol. For $\omega=0$ we have an eclipsed conformation generating a high steric hindrance and, consequently, a maximum in energy. A 60° rotation generates a conformation where the steric hindrance is minimized as well as the energy of the system. At this stage, the energy goes back to its eclipsed conformation (maximum) with a 120° rotation. Then the same energy variation repeats for additional two times going back to its original state after a three-fold repetition ($n=3$).

Such description is valid because every $H$ in ethane is equivalent and therefore minima and maxima are equivalent between each other, but obviously, this is not always the case. For example, rotation around single bonds in substituted systems generates different conformations (anti, gauche) corresponding to minima having different energies and barriers separating them (Figure 2). These effects can be considered by including an additional $n=1$ term in the torsional potential.

 

 

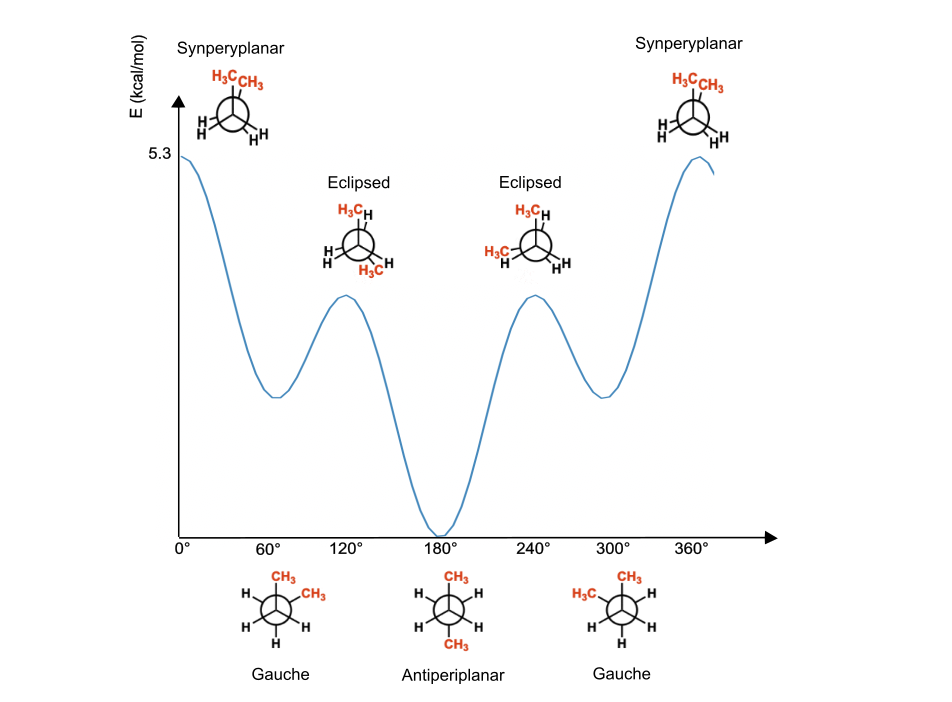
Figure 6. Torsional energy diagram in a single bond substituted system ($n=3$).

Rotation around double bonds must be periodic after 180° and, therefore, generates different energy variations with respect to the one we saw in the previous example, as their periodicity is $n=2$ and the energy curve repeats itself just two times in 360°. Another main difference is the energy barrier for rotations around double bonds that are much higher (larger $V_n$).
Also in this case, substituted double bonds generate alternative configurations cis and trans with distinct energies. In such cases, as already mentioned, we have to introduce another term in the expression. Therefore, we will result in a $V_2$ constant describing the $n=2$ periodicity rotation around the $C=C$ bond, and a $V_1$ determining the energy difference between the cis and trans isomers.

Overall the first three terms of the torsional potential are good enough to represent the vast majority of organic molecules.

 

$$E_{tors} = \frac{V_1}{2}(1 + cos(\omega))+ \frac{V_2}{2}(1 - cos(2\omega)) \frac{V_3}{2}(1 + cos(3\omega))$$

 

However, depending on the bond type we may insert just one term when parametrizing a force field aimed at large systems. Single bonds can be described by $cos(3\omega)$ and double bonds by $cos(2\omega)$.

 

Cross terms

 

In more sophisticated force fields we have some additional contributions named cross terms arising from the interaction between stretching, bending, and torsions. Indeed, when studying a molecule, we have to consider that all of the previous motions are not independent of each other.

As an example, let’s try to see what happens when we study a simple molecule such as $H_2O$ characterized by an equilibrium angle (104.5°) and a bond length of 0.958 A°. When the bond angle is decreased the equilibrium bond length elongates to 0.968 A°. Conversely, when the bond angle is widened the equilibrium bond length decreases.

This effect is not considered in the original expression for the potential energy. Therefore, to include the coupling between bond length and bond angle we need to introduce a so-called cross term. This term is written as a product of the Taylor series:

 

$$E_{str/bend} = k_{s/b} (\theta - \theta^0)[(l_1-l_1^0)(l_2-l_2^0)]$$

 

where $\theta$ is the angle, $l_1$ and $l_2$ are the two bond lengths.

Similarly, we can introduce additional cross terms considering the coupling between different molecular motions. The majority of them involve two internal coordinates but some force fields may involve three or more. For example, considering a generic $A-B-C-D$ molecule we can write:

 

$E_{str/bend} = k_{s/b} (\theta_{ABC} - \theta_{ABC}^0)[(l_{AB}-l_{AB}^0)(l_{BC}-l_{BC}^0)]$

$E_{str/str} = k_{s/s} (l_{AB}-l_{AB}^0)(l_{BC}-l_{BC}^0)$

$E_{bend/bend} = k_{b/b} (\theta_{ABC}-\theta_{ABC}^0)(\theta_{BCD}-\theta_{BCD}^0)$

$E_{str/tors} = k_{s/t} (l_{AB}-l_{AB}^0)cos(n\omega_{ABCD})$

$E_{bend/tors} = k_{b/t} (\theta_{ABC} - \theta_{ABC}^0)cos(n\omega_{ABCD})$

$E_{bend/tors/bend} = k_{b/t/b} (\theta_{ABC} - \theta_{ABC}^0)(\theta_{BCD} - \theta_{BCD}^0)cos(n\omega_{ABCD})$