Molecular Mechanics (MM)
A simple way to approximate molecules through the laws of classical mechanics
Molecular mechanics is a branch of computational chemistry that uses classical physics to simulate the behavior of molecules. It allows scientists to predict the structure, properties, and dynamics of molecules, as well as their interactions with other molecules and their environment. In this article, we will explore the basic principles of molecular mechanics and how it is used to study a wide range of chemical and biological systems.
Why Molecular Mechanics?
Quantum Mechanics (QM) or ab-initio methods are a remarkably powerful tool in molecular modeling. They allow us to take into account the quantum properties of atoms and construct a realistic model of microscopic systems (i.e., molecules in our case).
The main drawback of these methods is that they require long calculation times, especially for large molecules. As a result, many of the systems we consider in computational chemistry are unfortunately too large to be treated with QM methods in reasonable time scales.
This difficulty in applying ab-initio methods to large molecules has resulted in the development of classical-mechanics methods known as Molecular Mechanics (MM) or force-field methods.
These techniques allow us to speed up the calculations and, consequently, to perform analysis on systems containing significant numbers of atoms.
In MM, we ignore the quantum mechanical properties of the molecules and we simply consider them as atoms held together by bonds.
This so-called “ball and spring” model leads to a very rough approximation of the real properties of the system. Sometimes this is enough to provide some meaningful results, and useful information about the behaviour of large molecular systems, such as proteins.
Energy terms
The main idea behind MM methods is that we can ignore the electronic motions and calculate the energy of a molecule as a parametric function of the nuclear coordinates ($R$).
For a given conformation $R$, the molecular system’s potential energy can be expressed as a sum of different contributions:
$$ E_{MM}(R)=E_{str}+E_{bend}+E_{tors}+E_{cross}+E_{el}+E_{vdW} $$
Each term represents the change in energy due to:
- Stretching terms ($E_{str}$) $\Rightarrow$ Referring to the variations in bond length
- Bending terms ($E_{bend}$) $\Rightarrow$ Change in bond-angle
- Torsional terms ($E_{tors}$) $\Rightarrow$ Torsions about bonds
- Cross terms ($E_{cross}$) $\Rightarrow$ Interactions between the previous three motions
- Van der Waals ($E_{vdW}$) $\Rightarrow$ Van der Waals interactions between atoms
- Electrostatic ($E_{el}$) $\Rightarrow$ Polarization of the molecule
Comprehensively, the different contributions can be divided into two categories defined as Bonding terms and Non-bonding terms:
$$ E_{bond} = E_{str}+E_{bend}+E_{tors}+E_{cross} $$ $$ E_{non-bond} = E_{vdW}+E_{el} $$
Bonding terms are related to short-range interactions between atoms in 1-2, 1-3, and 1-4 relations (Figure 1). On the contrary, non-bonding terms account for long-range interactions between atoms connected by three or more bonds (1-5 relations or more).
While the number of bonding terms is proportional to the number of atoms of the system $N$, the number of non-bonding interactions increases as the square of the number of atoms $N^2$. For this reason, the most time-consuming part of building a molecular model is the computation of non-bonding interactions. To speed up the calculations we generally insert a cut-off distance. If the non-bonding interaction arises from a radius bigger than the cut-off we avoid computing that term.
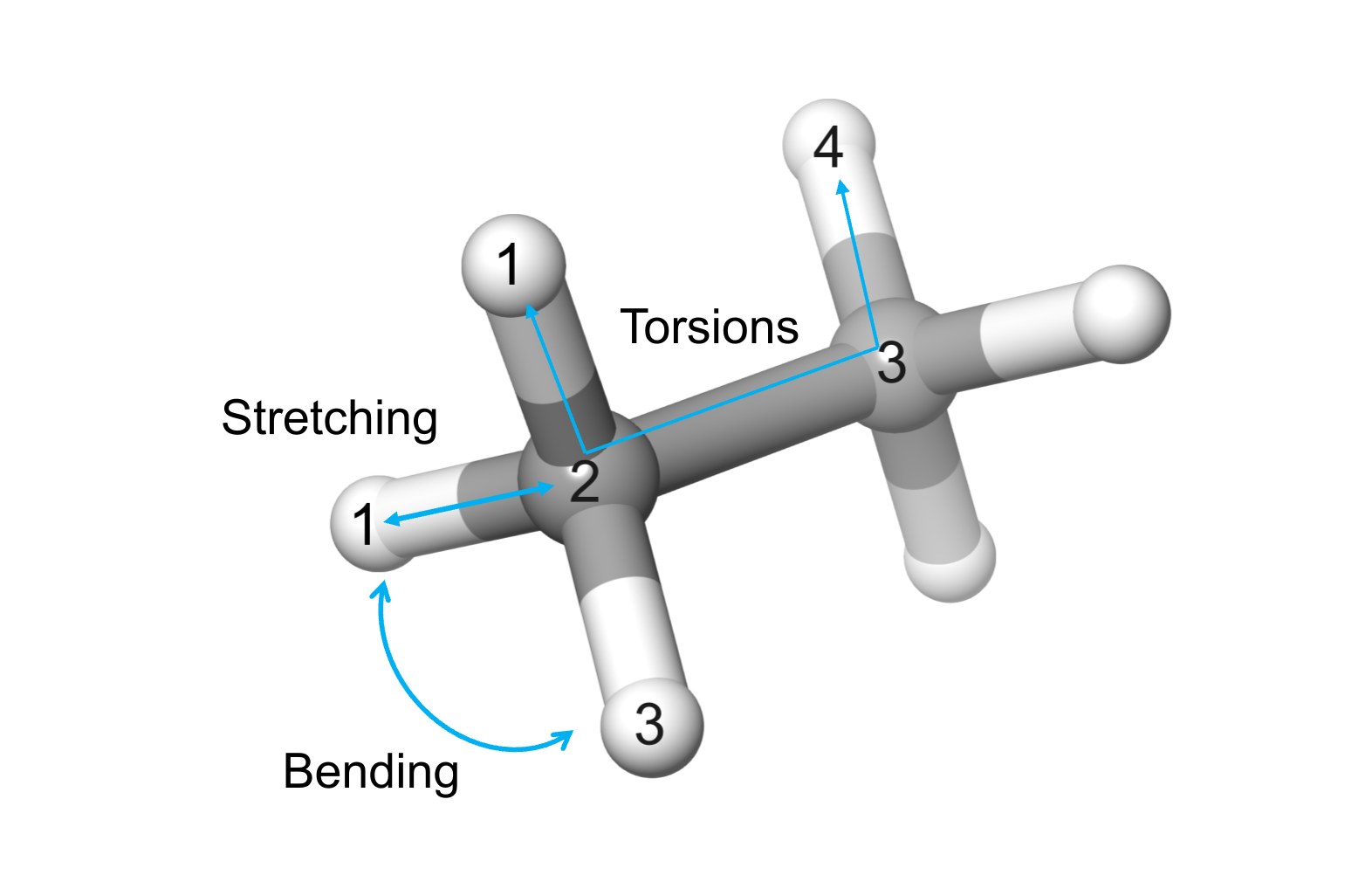
Figure 1. Simple illustration of the bonding terms in the molecular mechanics energy equation. In MM, atoms are considered as spheres having bonding ($E_{str}$, $E_{bend}$, $E_{tors}$), and non-bonding interactions ($E_{el}$, $E_{vdW}$) .
The essential idea of MM is that we can assign an energy value to each molecular configuration. The molecular structures characterized by lower energy values are the most stable ones, and vice versa. Therefore, by minimizing the expression of the energy for our molecule we can predict its equilibrium geometries.
A Molecular Mechanics representation of our system is generally a starting point for other methods. For instance, we can use the informations retrieved in MM to perform Molecular Dynamics simulation. In this way, we are not only able to determine the stable structure of the system, but also to observe how it evolves over time.
We can also use MM models to construct homology models, refine crystallographic structures, and perform Molecular Docking experiments.
As you may imagine, the fact that we do not account for the quantum mechanical properties of atoms could lead to some drawbacks. For instance, MM is not appropriate to describe the changes in the electronic structure of a system undergoing a chemical reaction. For this reason, ab-initio methods are still required when a more accurate description of a chemical process is needed.
Functional forms
The explicit expressions (functional form) used for each of the terms in the above equation, and the parameters contained inside them, define what is called a MM Force Field (FF). The most basic equation for a force field is the following:
$$ E_{MM}(R)= \sum_{bonds}\frac{k_i}{2}(l_i - l_{i,0})^2 + \sum_{angles}\frac{k_i}{2}(\theta_i - \theta_{i,0})^2 + \sum_{torsions}\frac{V_n}{2}(1 + cos(n\omega - \gamma)) + \sum_{i=1} \sum_{j=i+1}\left(4\epsilon_{ij}\left[\left(\frac{\theta_{ij}}{r_{ij}}\right)^{12}- \left(\frac{\theta_{ij}}{r_{ij}}\right)^{6}\right] + \frac{q_iq_j}{4\pi\epsilon_0r_{ij}}\right) $$
At a first glance, this equation may look terrifying. Don’t worry, you can find two dedicated articles treating both bonding terms and non-bonding terms in more detail.
In principle, for each atom in our system, we should compute the parameters contained in the equation. As you may imagine this is not really practical.
For this reason, a MM force field also divides all atoms into different categories named “atom types”, based on their atomic number and on the type of chemical bonding they are involved in. In this way, different atoms belonging to the same atom type will be treated with the same parameters.
Different force fields are currently available. One of the most widely used is the AMBER force field, which is designed for calculations on proteins and nucleic acids.
You can find further useful information on force fields here.